O poder das regras: menos partidos nas eleições de 2020
O alto número de partidos no Brasil é um assunto que faz parte das conversas cotidianas sobre política. Recentemente, o Congresso aprovou o fim das coligações para eleições proporcionais (Emenda Constitucional 97/2017), uma medida que tem potencial para reduzir o número de partidos ao longo dos anos, como expôs Jairo Nicolau em texto publicado no Observatório das Eleições/UOL.
As coligações para eleições proporcionais funcionavam de maneira que os votos de partidos coligados fossem somados. Assim, partidos pequenos podiam fazer alianças para sobreviverem na política. Com o fim dessa possibilidade, candidatas (os) a cargos proporcionais – vereadoras (es), por exemplo – tendem a concentrar suas forças em poucos partidos.
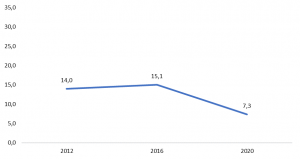
Gráfico 1. Número médio de partidos disputando cargos de vereadoras (es) por município
Fonte: Elaboração própria a partir de dados do Tribunal Superior Eleitoral (TSE).
O Gráfico 1 mostra a média do número de partidos disputando cargos de vereadoras (es) nos municípios brasileiros nos anos de 2012, 2016 e 2020. Neste ano, observa-se uma redução drástica dessa média, o que mostra a força da nova regra. No entanto, há diferenças entre municípios grandes e pequenos. Aplicando o corte de 200 mil eleitoras (es) – número utilizado pelo TSE para definir quais municípios terão segundo turno na disputa para prefeita (o) –, é possível observar que as cidades que ultrapassam esta marca têm uma média mais alta de partidos na disputa.
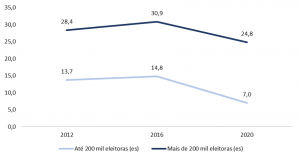
Gráfico 2. Número médio de partidos disputando cargos de vereadoras (es) por município – Recorte: 200 mil eleitoras (es)
Fonte: Elaboração própria a partir de dados do Tribunal Superior Eleitoral (TSE).
No Gráfico 2, nota-se que nos municípios maiores o número médio de partidos disputando cargos das Câmaras Municipais também passou por redução em 2020, mas ainda assim é mais alto que o observado em municípios menores. Uma das explicações para este fenômeno está no limite de candidaturas por chapa: para o cargo de vereador (a), cada partido só pode lançar um número de candidaturas que corresponda a 150% do número de vagas disponíveis (segundo a Lei nº 9.504/1997). Ou seja, em uma cidade com dez vagas na Câmara, um partido só pode lançar 15 candidaturas. Em municípios maiores, os partidos tendem a não preencher completamente suas chapas. Logo, há um “mercado” de votos maior, abrindo-se espaço para que mais legendas entrem na disputa.
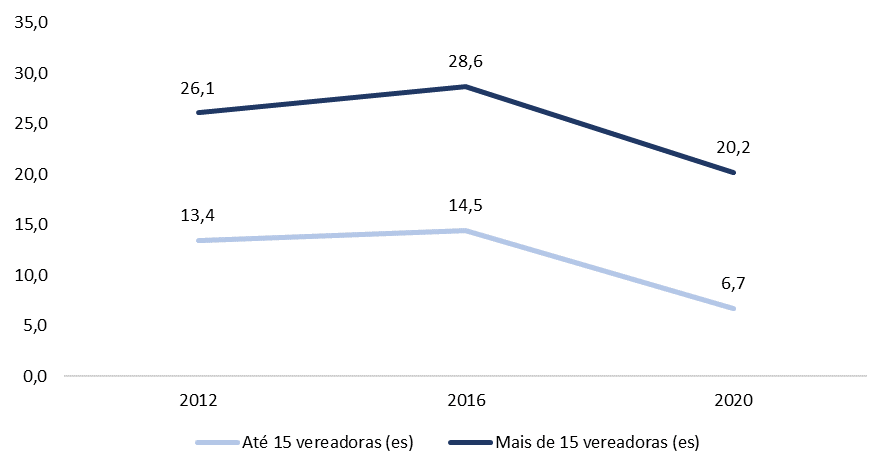
Nos municípios maiores, a média de cadeiras disponíveis nas Câmaras Municipais é de 23,8, podendo variar entre 15,9 e 31,7. Se separarmos os municípios que possuem 15 vagas ou menos, como foi feito no Gráfico 3, o número médio de partidos disputando vagas nos Legislativos municipais é ainda menor, atingindo 6,7 partidos em 2020. Em contrapartida, neste ano os municípios com 16 cadeiras ou mais possuem uma marca média de 20,2 legendas em disputa.
Gráfico 3. Número médio de partidos disputando cargos de vereadoras (es) por município – Recorte: 15 vagas na Câmara
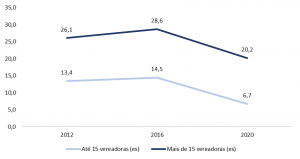
Fonte: Elaboração própria a partir de dados do Tribunal Superior Eleitoral (TSE). O número de vagas utilizado é referente ao ano de 2016, por não ser possível captar as variações que ocorreram nos municípios ao longo da última legislatura.
Em termos de estratégia, os partidos estão se adaptando à nova regra. As tendências são duas. Primeira, que o número de legendas nas competições reduza ao longo do tempo. Segunda, que essas legendas lancem o maior número possível de candidaturas, para reduzir os efeitos do fim das coligações.
Por fim, não se pode ignorar o fato de que o Brasil apresenta o sistema partidário mais fragmentado do mundo. Desta maneira, o fim das coligações proporcionais pode minar a força de um partido apenas em determinadas regiões, e ele pode sobreviver se tiver força em outras. Assim, um outro desdobramento possível para os próximos anos é um processo de regionalização dos partidos políticos brasileiros.
*Otávio Z. Catelano é Mestrando em Ciência Política na Unicamp e pesquisador do Centro de Estudos de Opinião Pública da Unicamp (Cesop/Unicamp).




